「うみねこのなく頃に」Episode 8中的Monty Hall问题思考
「うみねこのなく頃に」是我特别喜欢的一系列作品,也对我影响特别大。这部参照莎士比亚《无事生非》中人物设定的同人游戏,从出题篇的文笔的波诡云谲,再到解题篇的真相大白,其中的悬疑诡计、迷失推理堪称一绝。虽然龙7背离了本格推理的初心,再加上大部分人诟病的画风,但瑕不掩瑜,海猫依然在同人游戏史中留下浓墨重彩的一笔。
海猫解Episode8里,在战人给缘寿设计的棋盘中,喜庆的家庭会议上曾有一个分蛋糕情节,先让我们来回顾一下故事梗概:

乡田俊朗:“今天,作为今晚万圣节派对的亮点,我们特地准备了这个萨赫蛋糕。正如各位所看到的,这是用巧克力沾上单翼鹰纹章的封蜡,是右代宫家独有的一道菜!”
众人纷纷对那精美的蛋糕表示赞叹。

南条辉正:“这是个很棒的蛋糕啊...!真是吸引人眼球。”
乡田俊朗:“不不。不只是蛋糕哦。今晚的这个蛋糕有一个秘密。・・・・各位,请大家多多指教,多多关照!”
众人请缘寿先选。


此处引出了第一个问题:十五份蛋糕,其中一份有坚果,缘寿先选到的概率是十五分之一,后面是真里亚选,至此蛋糕便少了一块,此时便是十四分之一的概率,这之后的人的概率是十三分之一、十二分之一……,最后选的人一定会选到?六岁的缘寿简单地认为这样选是不公平的。可事实是这样的吗?
这是一个很简单的古典概型问题,关键就是在样本空间不变的情况下,不放回地抽取先验概率不变,这算是个生活常识,这里不再赘述。
剧情设定缘寿理所当然抽到了坚果,后来众人提议进行有奖问答,没人对缘寿问一个问题,答对便可以获得礼物。其中让治和朱志香的问题很值得深思,高中海猫一周目的时候,我这一点便没有想清楚。







题干:
有红色和蓝色的箱子和绿色的箱子。
其中一个有奖牌。
剩下的两个是可怕的惊吓箱。
我选了红色的箱子。
此时朱志香说:“你确定要选这个吗?惊吓箱很可怕的哦。不信打开一个给你看”
说着打开绿色的盒子,向我表明那是一个惊吓箱。
确实让人吓了一跳。
剩下的只有红色箱子和蓝色箱子两个。
“你还要打开那个红色的盒子吗?考不考虑换一个呢?“
那么,红色的箱子和蓝色的箱子。哪个有奖牌的概率比较高呢...?
这是一个经典的Monty Hall问题,原问题是这样的:
Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice?
假设你在一个游戏节目中,有三扇门可供选择:一扇门后面是一辆汽车;后面是山羊。你选了一扇门,说是1号门,主人知道门后面是什么,就打开另一扇门,说是3号门,门上有一只山羊。然后他对你说:“你想选2号门吗?”改变你的选择对你有利吗?
游戏中简化了这个结果→原因的概率问题,仅仅让比较那种该选择更有利,而我想从概率论的角度讨论一下这个问题,首先引出Rule of Elimination和Bayes’Theorem的概念:

Rule of Elimination

Bayes’Theorem
直觉是两个盒子概率一样,在一个惊吓箱被打开的情况下,剩下的箱子必然是一个惊吓箱,一个奖品箱,换不换似乎都一样。可惜答案是:换盒子的中奖概率更大。
先用古典概型的经典方法:
当缘寿转向另一个箱子而不是维持原先的选择时,中奖的概率将会加倍。
概率空间中有三种可能的情况,全部都有相等的可能性(1/3):
缘寿挑一号箱子,主持者挑二号箱子。转换将赢得奖励。
缘寿挑二号箱子,主持者挑一号箱子。转换将赢得奖励。
缘寿挑三号箱子,主持者挑一号箱子。转换将失败”,和“缘寿挑三号箱子,主持者挑二号箱子。转换将失败””此情况的可能性为:

故转换成功的概率是三分之二,显然高于不转换的概率。
接下来尝试用Bayes’Theorem来解决:
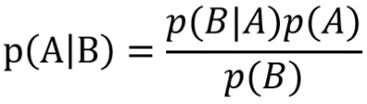
针对这个题目,我们假设有A、B、C三个箱子,缘寿选择了A箱子,朱志香打开了B门,然后要缘寿在A箱子和C箱子之间抉择换还是不换。那么如果奖品在B箱子里面,换与不换得到奖品的概率均为0,如果换了能赢,那么汽车必须在C箱子里面,现在我们求以下概率:

先看分母,显然有:
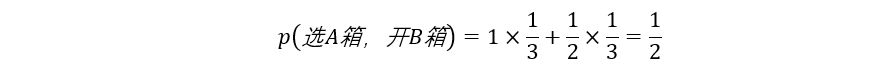
再看分子,当奖品在C箱子里时,缘寿选择了A箱子,朱志香只有B箱子可以打开,所以存在以下关系:

而奖品在C箱子的概率显而易见:

然后我们就求出了换箱子得到奖品的概率:

至此,问题结束。
最后,我利用Bayes’Theorem原理写了一个cpp程序验证
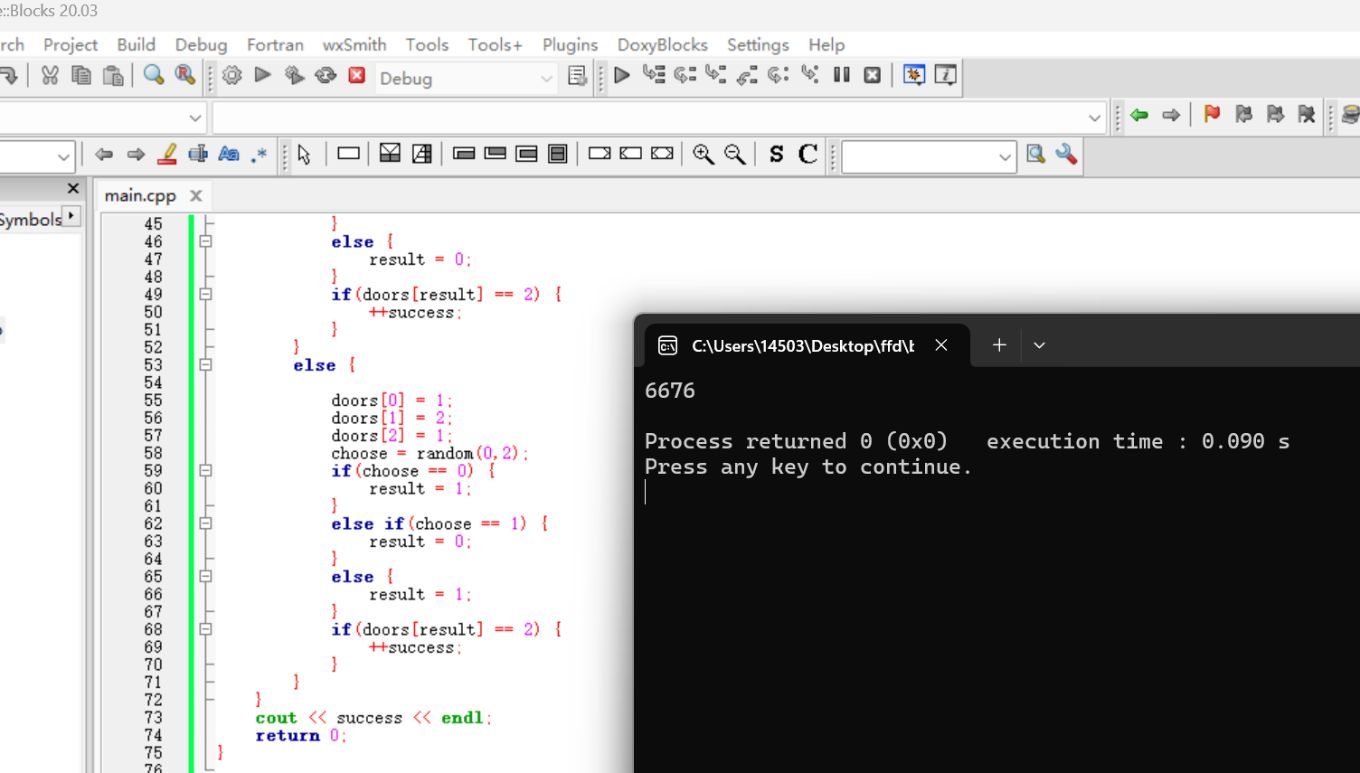
模拟一万次,输出结果为6676,与计算结果几乎一致。





回到游戏本身,盒子游戏引出了整个海猫中最精彩的对白之一,也是最令我印象深刻的点:
「あれは事後確率って言ってね。ある特定の情報を知ることで、あるいは知らないことで、確率が変動することを言うんだよ。」
「もし。10個のゲ-キの中にア-モンドが1つだった5、当たる確率は10%だね。…·でも、それが実は、100個のケ-キの中から適当に選んだ内の10個だと教えられたら”、どうなると思う?」
「縁寿ちやんが選んだゲ-キは何も変わらないのに。縁寿ちやんが何かを知ることによって、あるいは知らないことによって。縁寿ちやんのゲ-キの中に-アタリが生まれるかどうかの確率が、変化したんだよ。不思議な話だと思わないかい。」
「これから未来。様々な情報が、君の手の中のケ-キにそれらを知ることで、君のゲ-キの中干涉する。身は様々なものに変化するかもしれない。それは時に望むもの。…でも恐らく、それらのほとんどは、君の望まないものに変化するだるう。」
「君の中の真実は、最初から君の手の中にあるんだよ。そしてその中身は、実は君自身が決めているんだ。君が何を間き、何に耳を覆うかで、君自身がその中身を変化させている。」
「君の手の中の真実は、不変じやないんだ。それは君に対する様々な干渉で変化してしまう。·だからもし、君がその手の中の真実を大事にしたいと願うなら。」
"嘿,你知道吗,有时候做决定就跟挑蛋糕一样。比方说,你去咖啡店,看到有三块蛋糕,其中一块正好是你超爱的杏仁口味。你会觉得,我选的那块的中奖概率应该是三分之一吧?"
"但是,如果有人告诉你,其实这些蛋糕是从一百块里随机挑的十块,你会怎么想?你可能会犹豫,说不定我选的那块杏仁蛋糕还真没那么幸运呢?"
"虽然你选的蛋糕没变,但是因为知道了这个背景信息,你可能会开始怀疑自己的选择。也许觉得,中奖概率变小了,也可能会觉得,还是坚持原来的选择比较好。"
"所以,咱们得明白,我们做决定的时候,外界信息会对我们产生影响。有时候这些信息会让我们改变主意,有时候会让我们更加坚定自己的想法。"
"但最重要的是,无论什么情况,我们的真相其实一直在我们手里。我们的选择、我们的态度决定着最后的结果。只要我们保持警觉,不被外界左右,我们就能够保持真实的稳定。"
这是战人在棋盘中借助让治之口给缘寿的忠告,暗示她在以后继承了右代宫家业之时,有各种各样的势力、言语侵蚀她的内心,造谣六轩岛的悲剧,抹黑她已经逝去的家人,而战人希望她能够尊崇自己内心的真实而不动摇,这也是战人想通过Ep8棋盘中的Monty Hall游戏想传达的。
海猫的同人算是我接触到的国内质量最高的同人圈了,从音乐到棋盘都很精彩,龙7写海猫用了四年,我也花了三个多月才陆陆续续推完这四百万字的作品,从ep1的魔女棋盘到ep6的推理博弈再到ep8的感动,这一年很不容易,海猫和寒蝉可以算是我失落时、沮丧时坚持下去的动力。
这个故事,献给最爱的魔女贝阿朵莉切。

